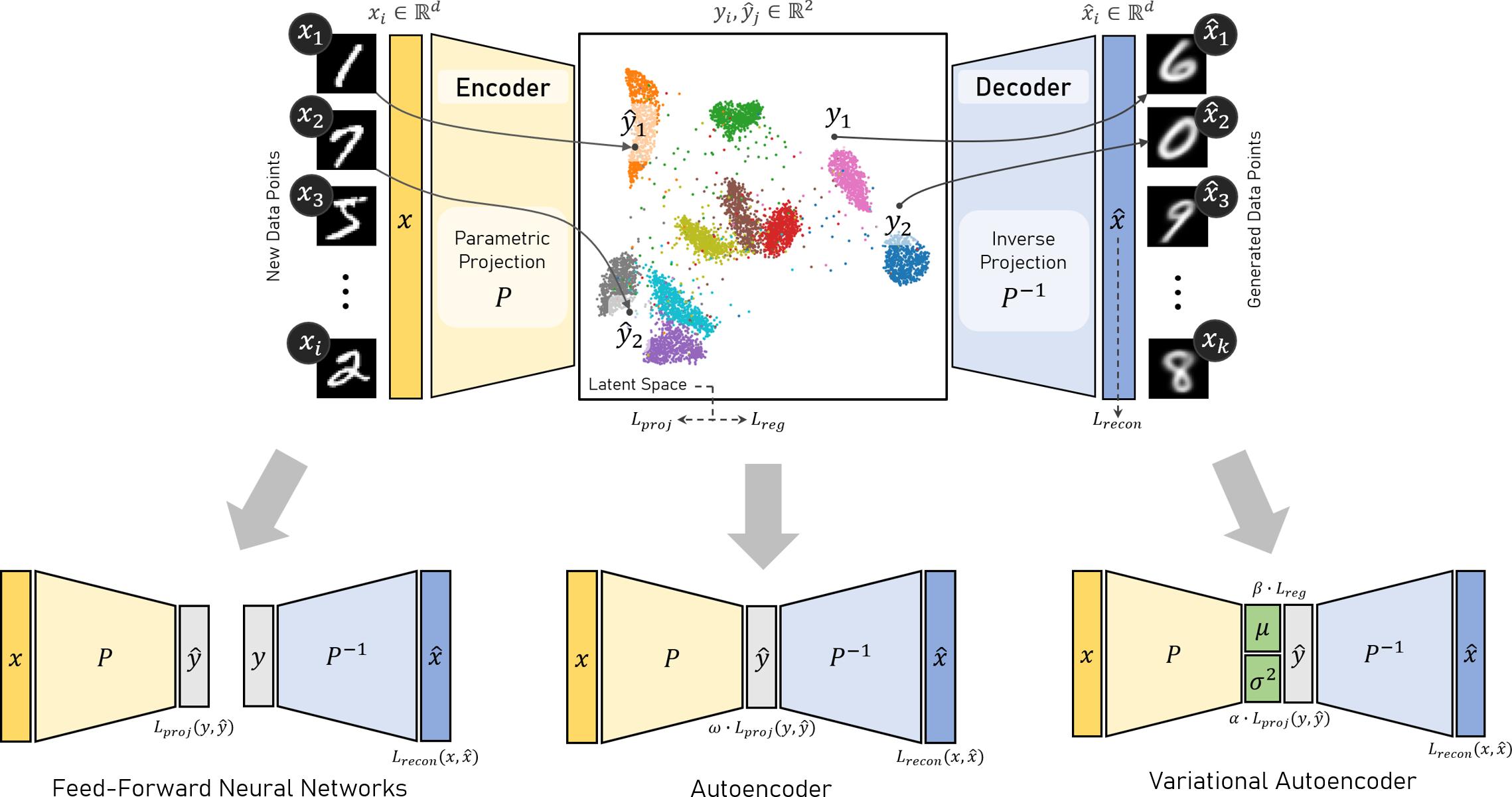
Abstract: Neural networks are used to create parametric and invertible multidimensional data projections. In this context, parametric projections enable the embedding of previously unseen data points without requiring a complete recomputation of the projection, while invertible projections allow for the reconstruction or generation of data in the original space. In this paper, we investigate the use of autoencoder (AE) architectures for simultaneously learning parametric and inverse mappings independent of the underlying dimensionality reduction method. We introduce and compare three regularization methods for autoencoder architectures designed to learn a forward mapping into two-dimensional space induced by the projection as well as inverse mappings back into the original feature space. To evaluate their performance, we conduct a systematic study on six datasets of varying dimensionality and structural complexity, using the established projection techniques t-SNE and UMAP as training targets. Our evaluation combines both quantitative metrics and qualitative assessments. The results demonstrate that AEs, particularly when trained with Kullback-Leibler divergence regularization, can achieve high-quality reconstructions while providing users with control over the degree of smoothing in the projection. Compared to disjoint neural networks, AE architectures yield superior generative capabilities for out-of-distribution samples, while still providing comparable reconstruction quality and parametric projection accuracy. This highlights their potential for interactive data generation in use cases such as classifier evaluation and counterfactual creation.